VAE 이해 및 pytorch 구현

0. 도움이 된 자료들

• 논문
• youtube 강의
• 블로그

1. 개요

Diffusion model에 대해 찾아보니 VAE(Variational Auto Encoder)와 관련된 개념이 많아 공부하게 되었다.
일단 전체적인 구조를 보면 다음과 같다.

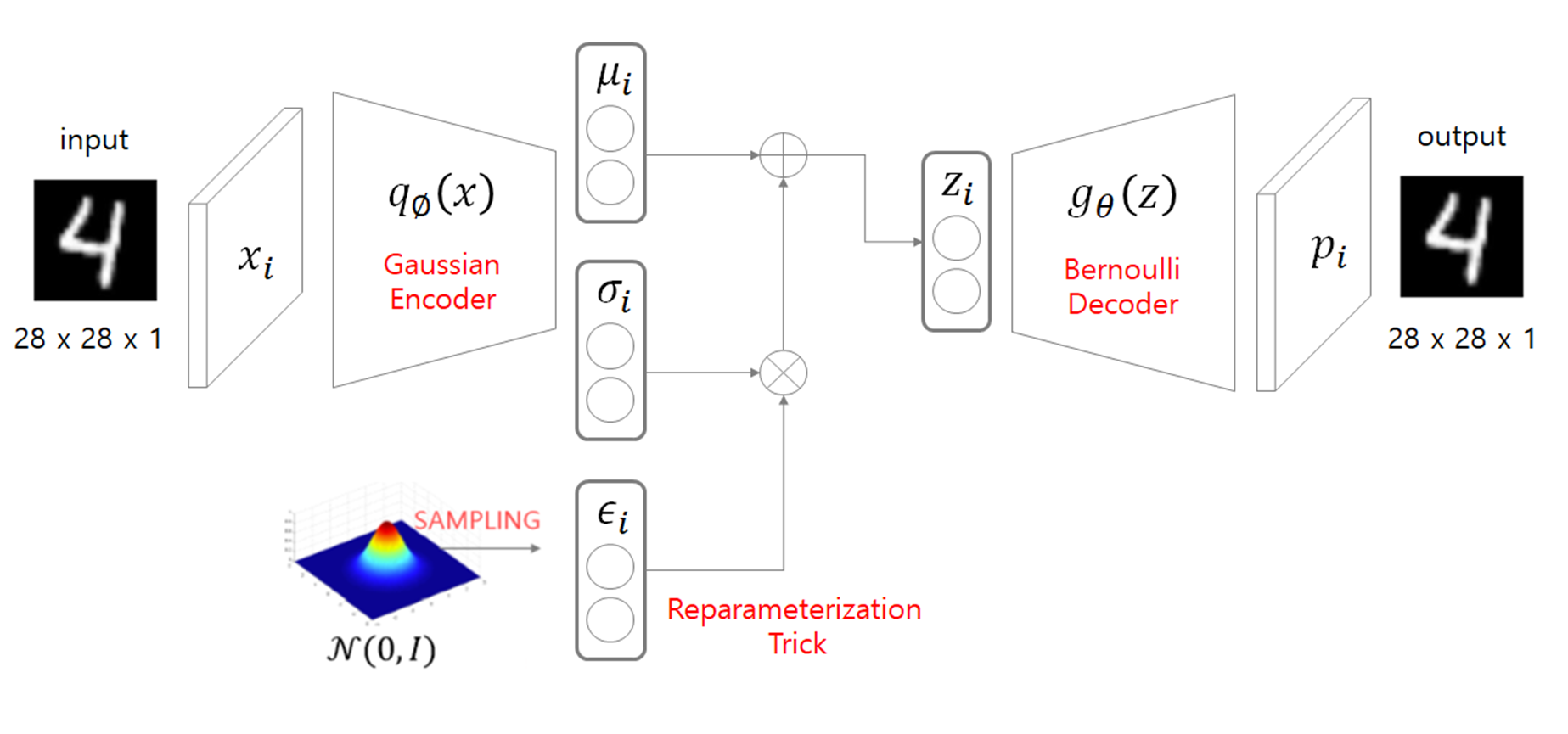
VAE는 개념상으로 Encoder 와 Decoder 로 이루어져있는데, 입력 데이터 $x_i$에 대해 각각의 역할을 다음으로 정리해 볼 수 있다.

Encoder
입력 $x_i$를 통해 확률공간$q_{\phi}(z_i \mid x_i)$을 만든다. 이 확률공간은 latent space로 사용되며 가우시안 분포의 형태를 가진다. 가우시안 분포를 만들기 위해선 평균과 표준편차가 필요하므로, 그림처럼 Encoder는 $x_i$를 통해 평균벡터$\mu_i$와 표준편차벡터$\sigma_i$를 생성한다.

Reparameterization Trick
Encoder가 생성해낸 latent space에서 latent vector인 $z_i$를 추출하는데 사용되는 방법이다. 이 과정이 필요한 이유는, Encoder가 생성해낸 두 벡터에 대한 연산을 정의해야 역전파시 미분이 가능해지기 때문이다.

Decoder
latent vector인 $z_i$를 통해 output을 생성해낸다.

2. VAE의 목적에 대해

논문의 Problem Scenario 를 보면 “주어진 데이터 $x_i$가 어떻게 생성되었을까?” 라는 질문과 그것에 대한 가정이 전제가 된다.

논문의 전제
$x_i$는 관측 불가하며 연속적인 $z$ 라는 랜덤 변수를 통해 생성된다. 완벽한 주어진 데이터에 대한 완전한 모방이 가능한 파라미터 $\theta^*$ 가 주어질때 $x_i$가 생성되는 과정은 다음과 같다.

1. 확률공간 $p_{\theta^*}(z)$에서 $z_i$ 가 생성된다.
2. $p_{\theta^*}(x \mid z)$에서 $x_i$가 생성된다.

VAE의 목표
주어진 데이터 $x_i$에 대해 $p_{\theta}(x_i)$를 최대화하는 파라미터 $\theta$를 찾는다.
즉 주어진 데이터와 가장 유사한 generative model을 생성하는것을 확률적으로 접근한 것 이다.

3. 모델링시의 문제점 및 Encoder의 도입

2번을 통해 $p_{\theta}(x)$를 최대화 시키는것이 VAE의 목적임을 알았다. 하지만 $p_{\theta}(x)$를 직접 모델링하는데에는 몇가지 걸림돌이 있다.

1. $p_{\theta}(x) \, = \, \int{p_{\theta}(z)p_{\theta}(x\mid z)dz}$ 가 계산 불가하다.
2. 베이즈 정리로 계산할 시 $p_{\theta}(x) \, = \, \frac{p_{\theta}(x \mid z)p_{\theta}(z)}{p_{\theta}(z \mid x)}$ 인데, $z$가 알려져 있지 않기 때문에 $p_{\theta}(z \mid x)$와 $p_{\theta}(z)$를 직접 구할 수 없다.

위의 문제점을 해결하기 위해 VAE는 Encoder($q_{\phi}(z \mid x)$)를 통해 $p_{\theta}(z \mid x)$를 모방한다.
따라서 VAE는 Encoder를 통해 추출된 $z$를 기반으로 $p_{\theta}(x)$를 최대화하는 목표를 가진다.
수식으로 나타내면 $E_{z \sim q_{\phi}(z \mid x)}[p_{\theta}(x)]$를 최대화 하는것.

4. Loss 유도 - Lower bound

$E_{z \sim q_{\phi}(z \mid x)}[ p_{\theta}(x)]$를 최대화 하는것은 $E_{z \sim q_{\phi}(z \mid x)}[ \log p_{\theta}(x) ]$를 최대화 하는것과 같다.
여기서 KL은 kullback leibler divergence를 의미한다.

\(E_{z \sim q_{\phi}(z \mid x)}[ \log p_{\theta}(x) ] = E_{z}[ \log p_{\theta}(x \mid z) ] - E_{z}[ \log \frac{q_{\phi}(z \mid x)}{p_{\theta}(z)} ] + E_{z}[ \log \frac{q_{\phi}(z \mid x)}{p_{\theta}(z \mid x)} ] \\ = E_{z}[ \log p_{\theta}(x \mid z) ] - \int q_{\phi}(z \mid x) \log \frac{q_{\phi}(z \mid x)}{p_{\theta}(z)} dz + \int q_{\phi}(z \mid x) \log \frac{q_{\phi}(z \mid x)}{p_{\theta}(z \mid x)} \\ = E_{z}[ \log p_{\theta}(x \mid z) ] - KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z)) + KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z \mid x))\)
위처럼 계산된 수식에 아래의 두 가지 요인을 적용하여 loss를 단순화 한다.

• kullback leibler divergence는 항상 0 이상의 값이다.
• $p_{\theta}(z \mid x)$는 계산 불가하다.

따라서 마지막 항을 제거하고 $E_{z \sim q_{\phi}(z \mid x)}[ \log p_{\theta}(x) ]$의 하한값을 최대화 시키는 문제로 수식을 변형 할 수 있다.

최종적으로 lower bound로서 loss를 정의할 수 있다.
\(E_{z \sim q_{\phi}(z \mid x)}[ \log p_{\theta}(x) ] \ge E_{z}[ \log p_{\theta}(x \mid z) ] - KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z))\)

5. Loss 계산

\(E_{z}[ \log p_{\theta}(x \mid z) ] - KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z))\)
위 수식을 최대화 하는 문제를 아래의 값을 최소화 시키는것 으로 변형 할 수 있다.(일반적인 loss를 계산할 때 처럼) \({-} E_{z}[ \log p_{\theta}(x \mid z) ] + KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z))\)
이제 각각의 항들을 계산하면된다. 각 항은 모델의 출력값과 입력값을 비교하는 Reconstruction Error 와 Encoder가 만들어내는 분포와 $p_{\theta}(z)$의 차이를 줄이는 Regularization 으로 볼 수 있다.

5.1 Reconstruction Error: ${-} E_{z}[ \log p_{\theta}(x \mid z) ]$

\({-} E_{z \sim q_{\phi}(z \mid x)}[ \log p_{\theta}(x \mid z) ] = - \int q_{\phi}(z \mid x) \log p_{\theta}(x \mid z) dz\) 위에서 모든 $z$에 대한 계산이 불가능하기 때문에 Monte-carlo technique를 사용한다. 이 방법은 전체 $z$를 구하는대신에 $L$개의 $z$에 대한 계산만 진행하는것 이다.
VAE는 $L$을 1로 두고 계산한다. \({-} \log p_{\theta}(x \mid z)\)

계산하기 위해 또 생각해야할 것이 있는데, 바로 $x$의 분포이다. $x_i$가 주어진 입력 데이터 벡터일때.

$x_i$의 각 값들이 Bernoulli Distribution이라 가정하면
모델의 출력은 $p_i$라는 하나의 벡터가 되야한다. Reconstruction Error는 Cross Entropy로 유도된다.
\({-} \log p_{\theta}(x_i \mid z_i) = - \log ( \prod_{j=1}^D p_{\theta}(x_{i, j} \mid z_i)) = - \sum_{j=1}^D \log(p_{\theta}(x_{i, j} \mid z_i)) = - \sum_{j=1}^D \log(p_{i,j}^{x_{i,j}}(1-p_{i,j})^{1-x_{i,j}}) = - \sum_{j=1}^D \{ x_{i,j}\log p_{i,j} + (1 - x_{i,j}) \log (1-p_{i,j}) \}\)

$x_i$의 각 값들이 Gaussian Distribution이라 가정하면
모델은 $\acute{\mu_i}$와 $\acute{\sigma_i}$ 두 벡터를 출력해야한다. Reconstruction Error는 표준편차가 1일때 MSE가 된다.
\({-} E_{z}[ \log p_{\theta}(x \mid z) ] \approx {-} \log p_{\theta}(x_i \mid z_i) = - \log ( \mathcal{N}(x_i; \acute{\mu_i}, \acute{\sigma_i}^2 I) ) = \sum_{j=1}^{D} \{ \frac{1}{2} \log \acute{\sigma_{i,j}}^2 + \frac{(x_{i,j} - \acute{\mu_{i,j}})^2}{2 \acute{\sigma_{i,j}}^2} \}\)

5.2. Regularization: $KL(q_{\phi}(z \mid x) \mid \mid p_{\theta}(z))$

위 항을 최소화하는데 두가지 가정이 필요하다.

• $p_{\theta}(z) = \mathcal{N}(0, I)$
• $q_{\phi}(z \mid x)$는 $\mathcal{N}(\mu_i, \sigma_i^2 I)$로 표현 가능하다
  • Encoder의 출력은 $\mu_i$ 벡터와 $\sigma_i$ 벡터이다.

위 두 가정을 통해 Regularization식을 $\mu_i$ 벡터와 $\sigma_i$ 벡터에 대한 식으로 변형 가능하다. \(KL(q_{\phi}(z_i \mid x_i) \mid \mid p_{\theta}(z_i)) = KL(\mathcal{N}(\mu_i, \sigma_i^2 I) \mid \mid p_{\theta}(z_i)) = \frac{1}{2} \sum_{j=1}^J \{ \mu_{i,j}^2 + \sigma_{i,j}^2 - \ln (\sigma_{i,j}^2) - 1 \}\)

6. Loss 정리

6.1. Gaussian Encoder + Bernoulli Decoder

각 input data $x_i$에 대해. \(Loss = {-} \sum_{j=1}^D \{ x_{i,j}\log p_{i,j} + (1 - x_{i,j})\log(1 - p_{i,j}) \} + \frac{1}{2}\sum_{j=1}^J\{ \mu_{i,j}^2 + \sigma_{i,j}^2 - \ln(\sigma_{i,j}^2) - 1 \}\) 이때 $\mu_{i,j}, \sigma_{i,j}, \epsilon_i \in R^J$ 이고 $x_i, p_i \in R^D$ 이다.

6.2. Gaussian Encoder + Gaussian Decoder

각 input data $x_i$에 대해. \(Loss = \sum_{j=1}^{D} \{ \frac{1}{2} \log \acute{\sigma_{i,j}}^2 + \frac{(x_{i,j} - \acute{\mu_{i,j}})^2}{2 \acute{\sigma_{i,j}}^2} \} + \frac{1}{2}\sum_{j=1}^J\{ \mu_{i,j}^2 + \sigma_{i,j}^2 - \ln(\sigma_{i,j}^2) - 1 \}\) 이때 $\mu_{i,j}, \sigma_{i,j}, \epsilon_i \in R^J$ 이고 $x_i,\acute{\mu_i}, \acute{\sigma_i} \in R^D$ 이다.

7. VAE 개념 정리

• VAE의 목적 - 어떤 데이터 $x$가 주어졌을때, $p_{\theta}(x)$를 최대화하는 parameter인 $\theta$를 찾고싶다.
• 베이즈 정리를 통해서 $p_{\theta}(x) = \frac{p_{\theta}(x \mid z) p_{\theta}(z)}{p_{\theta}(z \mid x)}$ 를 유도할 수 있다.
• $z$는 $x$에서 추출한 latent vector로 생각하고 $p_{\theta}(z) \approx \mathcal{N}(0, I)$로 가정한다.
• $z$를 추출하기 위해 $p_{\theta}(z \mid x)$를 모방하는 $q_{\phi}(z \mid x)$인 Encoder를 사용한다.
  • $p_{\theta}(x)$를 최대화하는 문제를 $E_{z \sim q_{\phi}(z \mid x)}[p_{\theta}(x)]$를 최대화하는 문제로 바꾼다.
• Encoder의 학습을 위해 reparameterization technique를 사용한다.

8. 구현

Gaussian Encoder + Bernoulli Decoder를 pytorch로 구현해봤다.

8.1. MLP Network

import torch.nn as nn
import torch

class BernoulliMLP(nn.Module):
    
    def __init__(self, device):
        super(BernoulliMLP, self).__init__()
        
        self.device = device
        self.J = 10 # Encoder가 출력하는 벡터들의 크기
        self.D = 116412 # 입력 벡터의 크기 ex. (3, 218, 178)의 사이즈를 가지는 이미지

        self.encoder = nn.Sequential(
            nn.Linear(in_features=116412, out_features=1164),
            nn.ReLU(),
            nn.Linear(in_features=1164, out_features=116),
            nn.ReLU(),
            nn.Linear(in_features=116, out_features=self.J * 2)
        )
        
        
        self.decoder = nn.Sequential(
            nn.Linear(in_features=self.J, out_features=116),
            nn.ReLU(),
            nn.Linear(in_features=116, out_features=1164),
            nn.ReLU(),
            nn.Linear(in_features=1164, out_features=116412)
        )
        
        
    def forward(self, x):
        
        batch_size = len(x)
        x = x.view(batch_size, -1)
        
        ####
        # Encoder에서 평균과 표준편차 벡터를 추출한다.
        ####
        code = self.encoder(x) # [batch, J * 2]
        mean, std = code[:, 0 : self.J], code[:, self.J : ]
        
        ####
        # 벡터 z를 추출하기 위해 표준정규분포에서 epsilon을 추출한다.
        ####
        epsilon = torch.normal(mean=torch.zeros(size=(batch_size, self.J)), std=torch.ones(size=(batch_size, self.J))).to(self.device)
        
        ####
        # reparameterization technique
        ####
        z = mean + std * epsilon

        ####
        # Decoder로 출력값을 얻는다.
        # 이때 Bernoulli 분포의 값은 0혹은 1 이므로 둘 사이의 값이 되도록 sigmoid를 적용한다.
        ####
        p = self.decoder(z)
        p = torch.sigmoid(p)

        return p, mean, std

8.2. Loss

import torch.nn as nn
import torch

class BernoulliLoss(nn.Module):
    
    def __init__(self):
        super(BernoulliLoss, self).__init__()
        
    def forward(self, x, p, mean, std):
        """_summary_
        아래의 직접
        Args:
            x (_type_): input data
            p (_type_): output of bernoulli decoder
            mean (_type_): mean tensor from gaussian encoder
            std (_type_): std tensor from gaussian encoder
        """
        batch_size = len(x)
        x = torch.flatten(input=x, start_dim=1) # 배치단위이기 때문에 dim=1 부터 flatten
        p = torch.flatten(input=p, start_dim=1)
        
        
        reconstruction_err = - (1 - x) * torch.log(1 - p + 1e-8) - x * torch.log(p + 1e-8)
        reconstruction_err = torch.sum(reconstruction_err)
        
        regularization_err = 0.5 * (mean**2 + std**2 - torch.log(std**2 + 1e-8) - 1)
        regularization_err = torch.sum(regularization_err)
        
        return (reconstruction_err + regularization_err) / batch_size