Rst
[백준 1725번 히스토그램] JAVA 풀이
문제 요구사항
문제 링크
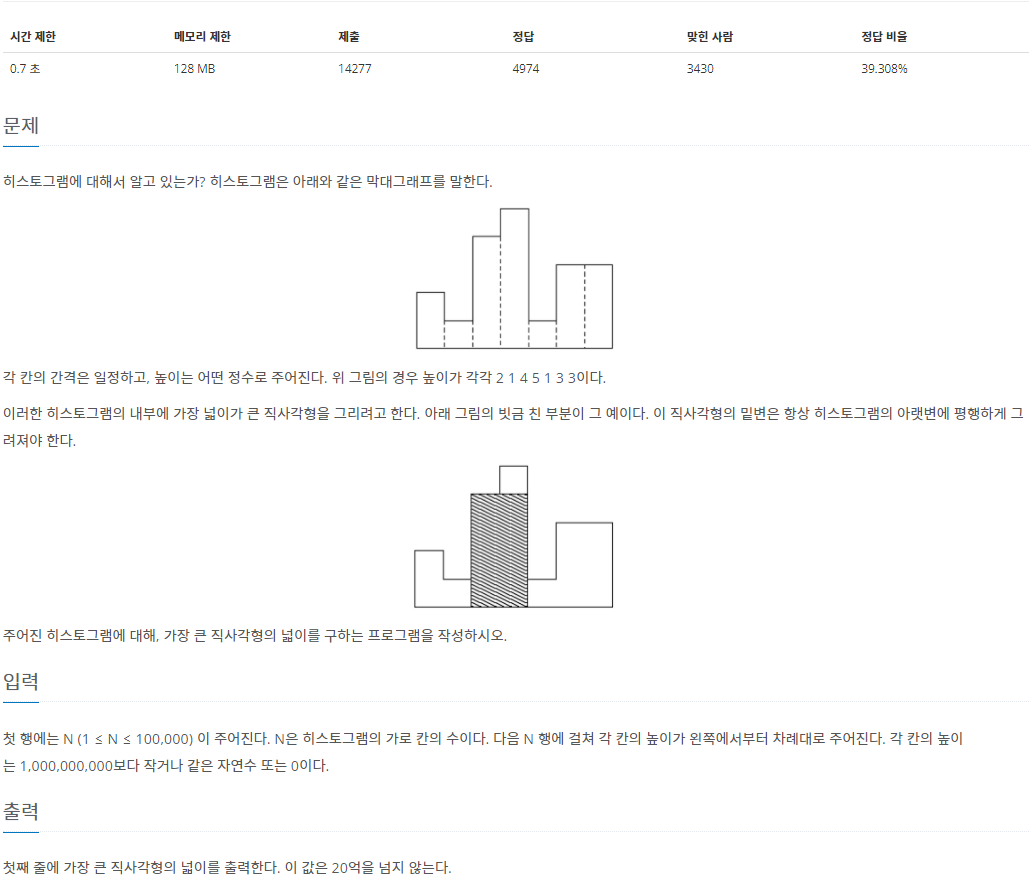히스토그램에서 밑변과 평행한 가장 큰 직사각형을 그리는것이 문제다.
이때 직사각형의 높이는 히스토그램의 높이보다 높을 수 없으므로 직사각형이 걸쳐있는 여러개의 막대중 가장 작은 막대의 높이와 같을 것 이다.
직사각형이 어떤 형태를 가져야하는지 알았으니 어떻게 가장 큰 직사각형을 판단할지 정해야한다.
직사각형 구하기
직사각형을 분류하자면 아래의 3가지중 하나이다.
- 전체 히스토그램의 가운데에 걸쳐있는 경우
- 히스토그램의 왼쪽 절반에 위치해 있는경우
- 히스토그램의 오른쪽 절반에 위치해 있는경우
이러한 분류를 하면 왼쪽의 직사각형, 오른쪽의 직사각형, 가운데에 걸친 직사각형 3가지를 각각 구한다음 비교하면된다. 이때, 시간복잡도는 Nlog(N)인데 N이 크지 않으므로 제한시간안에 풀이가 가능하다.
또, 이 분류의 장점은 전체 문제를 작은 문제로 나눌수 있으며 재귀적인 방법으로 구할 수 있다는것이다.
재귀적으로 구할 때 주의할 점은 기저사례를 놓치지 않는것인데 나는 이 문제의 기저사례를 막대 하나에 대해서만 직사각형을 구할때로 적용했다.
소스코드
import java.io.*;
import java.util.*;
public class 히스토그램1725 {
/**
* https://www.acmicpc.net/problem/1725
*
* 큰 막대 부터 시작
*/
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
histogram = new long[N];
for(int i = 0; i < N; i++) histogram[i] = Integer.parseInt(br.readLine());
System.out.println(find(0, N - 1));
}
static long[] histogram;
/**
* start부터 end중에 가장 큰 직사각형 구한다.
*/
static long find(int start, int end){
if(start == end) return histogram[start];
int mid = (start + end) / 2;
//왼쪽
long result = find(start, mid);
//오른쪽
result = Math.max(result, find(mid + 1, end));
//중간에 걸친(큰 막대에서부터 구하기)
if(histogram[mid] < histogram[mid + 1]) mid++;
int s = mid; int e = mid;
long min = histogram[mid];//막대중 최소 높이
while(s >= start && e <= end){
result = Math.max(result, min * (e - s + 1));
if(e == end && s == start) break;
if(e == end){s--; min = Math.min(min, histogram[s]);continue;}
if(s == start){e++; min = Math.min(min, histogram[e]);continue;}
//왼쪽, 오른쪽중 더 큰 막대의 방향으로 이동
if(histogram[s - 1] < histogram[e + 1]){e++; min = Math.min(min, histogram[e]);}
else{s--; min = Math.min(min, histogram[s]);}
}
return result;
}
}
Feel free to share!