Residual Learning Concepts

I'm going to organize a few key concepts from "Deep Residual Learning for Image Recognition" by Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun.

1. What is the problem
2. How to solve the problem
3. Residual Learning
4. Identity Mapping by Short cuts
5. Deeper Bottleneck Architecture

1. What is the problem

The depth of a network is an important factor that determines its performance in deep learning. However, deepening the network can cause the vanishing or exploding gradient problem. To solve this, solutions such as Batch Norm and weight initialization were introduced.

Although these solutions allowed deeper networks to converge, the training error did not decrease.

2. How to solve the problem

The authors believe that the problem is due to the difficulty of optimizing deeper layers, not overfitting.
They ask the question, "If deeper layers act like an identity function, would the training error drop?" The answer is Residual Learning and Shortcut connections.

3. Residual Learning

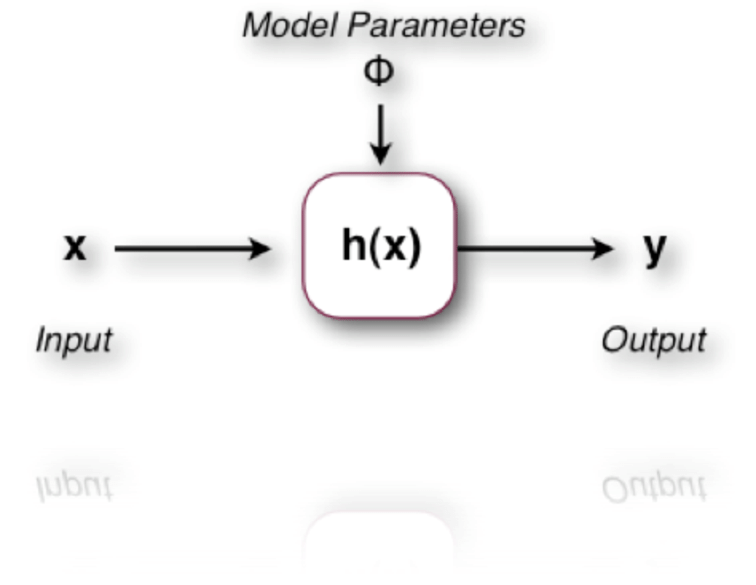
In deep learning, each building block of a model has its own function h(x) for the input x.

The authors suggest that if a block can learn the function h(x), it can also learn the residual function F(x) = h(x) - x.

Using a residual function with an identity mapping (F(x) + x) produces the same output as before, but the difficulty of optimization is different.

for example, if the identity mapping is optimal, the block only has to produce an output of zero. As a result, residual learning with an optimal identity mapping does not exceed the training error of a shallow network.

4. Identity mapping by shortcuts

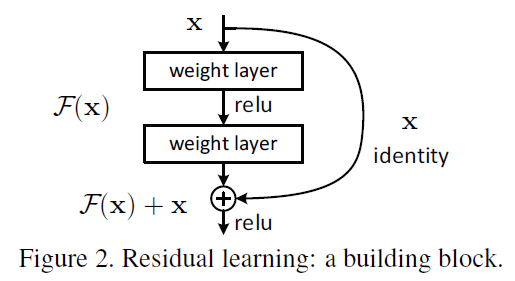
The paper describes two types of identity mapping

• no size difference between input and output
• size difference between input and output

1. no size difference
$Y \, = \, F(X, \, {W_i}) \, + \, X$
there is no need to change the input size, and the output is the sum of the input and the residual function (F: output of the building block).

2. size difference
$Y \, = \, F(X, \, {W_i}) \, + \, W_sX \,\,\,(W_s:projection)$
the input size needs to be changed, and the output is produced by projecting the input.

etc
In other studies, it is shown that identity mapping addresses the vanishing / exploding gradient problem.

5. Deeper Bottleneck Architecture

The right one of below image is an example of bottleneck architecture.

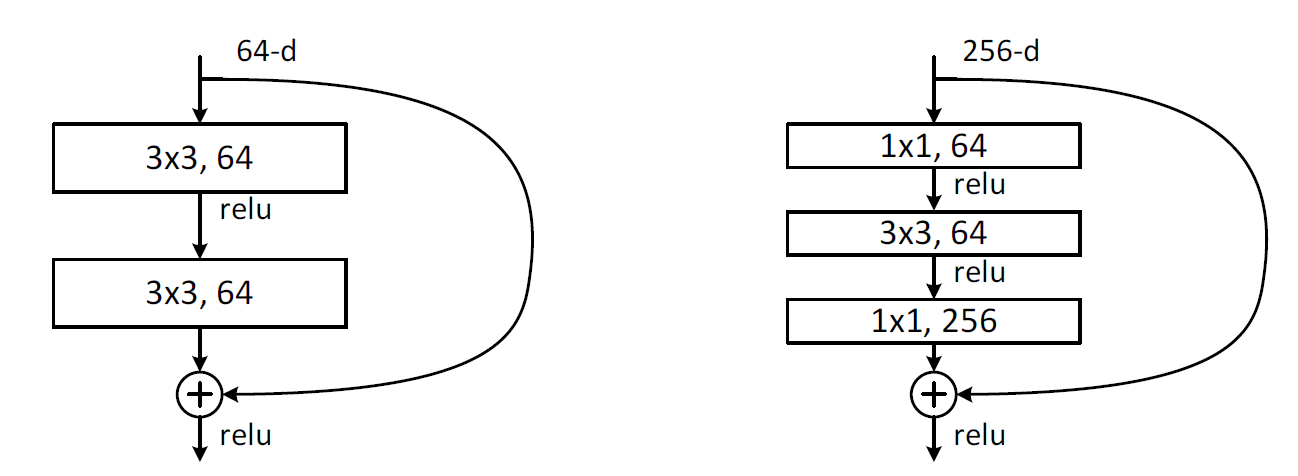
A bottleneck architecture reduces the dimensionality of the input while maintaining that of the output.

why use bottleneck?
By reducing dimensionality of input, number of computation in building block can be decreased, and less computation leads to time efficiency.

Role of each layer of bottleneck architecture

• first 1x1 conv
  • reducing dimension (compressing)
• 3x3 conv
  • maintaing dimension
• final 1x1 conv
  • increasing dimension (restoring)